<svg version="1.1" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" x="0" y="0" viewBox="0 0 27.4 20" class="svg-quote" xml:space="preserve" style="fill:#666; display:block; width:28px; height:20px; margin-bottom:10px"><path class="st0" d="M0,12.9C0,0.2,12.4,0,12.4,0C6.7,3.2,7.8,6.2,7.5,8.5c2.8,0.4,5,2.9,5,5.9c0,3.6-2.9,5.7-5.9,5.7 C3.2,20,0,17.4,0,12.9z M14.8,12.9C14.8,0.2,27.2,0,27.2,0c-5.7,3.2-4.6,6.2-4.8,8.5c2.8,0.4,5,2.9,5,5.9c0,3.6-2.9,5.7-5.9,5.7 C18,20,14.8,17.4,14.8,12.9z"></path></svg>i라는 문항이 제시되었을 때 … i문항에 응답하는 경향(Γi)은 피험자의 능력(θ)에 따라 정규 분포로 그려지게 될 것이고, 문항의 난이도가 i일 때 Γi가 이보다 높으면 문항의 답을 맞히게 될 것이다. 즉 <그림1>과 같이 θ가 -1.3, 0, 1.5일 때 각각의 정규 분포가 그려진다면 i보다 위에 있는 면적이 문항의 답을 맞힐 확률이 되어, θ가 -1.3인 집단의 답을 맞힐 확률은 0.2, θ가 0인 집단의 답을 맞힐 확률은 0.5, θ가 1.5인 집단의 답을 맞힐 확률은 0.92로 얻어진다. 이런 방식으로 각 능력에서 문항의 답을 맞힐 확률인 P(θ)를 구하고, 이를 연결하는 곡선을 그리면 <그림2>와 같은 문항 특성 곡선이 나타난다.
문항 특성 곡선은 능력이 낮은 집단의 P(θ)는 낮고, 능력이 높은 집단의 P(θ)는 높음을 나타내는 증가함수다. 문항 특성 곡선에서 문항의 난이도는 위치 모수로 나타난다. 위치 모수는 문항의 P(θ)가 0.5일 때 그에 대응하는 지점을 의미한다. 위치 모수는 오른쪽에 있을수록 어려운 문항으로 추정된다. 반면 문항의 변별도는 척도 모수로 나타난다. 척도 모수는 문항 특성 곡선의 기울기가 가파를수록 높다고 추정된다.
(Γi)은 …(θ)에 따라 정규 분포로 그려지게 …일 때 …으면 …게 될 … 즉 <그림1>과 같이
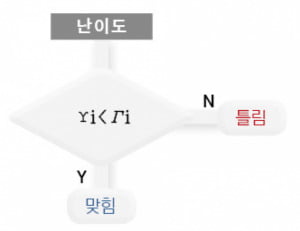함수와 그것의 표현인 그래프는 수학적 사고로서, 국어 능력이라 했다. ‘A는 B에 따라 (그래프)로 그려지다’라는 문장은 함수를 나타낸다. 지문에서 ‘i문항에 응답하는 경향(Γi)은 피험자의 능력(θ)에 따라 정규 분포로 그려지’다고 했는데, 이는 ‘피험자의 능력(θ)’을 독립 변수, ‘i문항에 응답하는 경향(Γi)’을 종속 변수로 하는 함수임을 말한 것이다. 한편 ‘정규 분포’는 도수(度數) 분포 곡선이 평균값을 중앙으로 하여 좌우 대칭인 분포로서, 종 모양의 그래프로 표현된다. 이는 확률과 통계 교과 때 배우는 개념이므로 고등학생이면 ‘알고 있어야’ 한다. 또 ‘난이도가 i일 때 Γi가 이보다 높으면 문항의 답을 맞’힌다는 내용은 옆의 판정도를 그려가며 이해하면 좋다.그래프를 보는 훈련이 필요하다.
우선 <그림1>에서 x축이 θ, y축이 Γi인 것을 확인해야 한다. 독립 변수와 종속 변수를 확인하는 것이다. ‘정규 분포’의 의미를 바탕으로 종 모양이 세로로 된 3개의 도형을 확인해야 한다. 그래프 모양은 여러 가지 정보를 전달하기 때문이다. 앞에서 내린 판정을 3개의 도형에서 빗금 친 부분을 통해 확인하고, ‘θ가 -1.3인 확률은 0.2, θ가 0인 확률은 0.5, θ가 1.5인 확률은 0.92로 얻어진다’는 내용은 <그림2>에 있는 각각의 수의 위치에 동그라미를 하며 확인해야 한다.
각 능력에서 … P(θ)를 구하고, 이를 연결하는 곡선을 그리면 … 문항 특성 곡선이 나타난다. … 문항 특성 곡선은 … 증가함수이다.
수많은 순서쌍(두 집합의 원소에 순서를 주어서 만든 짝)들이 모인 것이 그래프라 했다. 이를 알고 있으면 지문을 읽으며 ‘능력’ 집합의 원소와 ‘P(θ)’ 집합의 원소들로 된 순서쌍의 집합이 문항 특성 곡선임을 이해할 수 있다.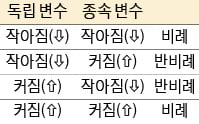
함수에서 꼭 파악해야 하는 것이 옆의 표와 같은 ‘(정)비례’, ‘반비례’라고 했다. 지문에서 말하는 ‘증가함수’는 변수들이 비례 관계에 있음을 말한다. 이는 <그림2>처럼 그래프가 우상향 형태로 표현된다. ‘능력이 낮은 집단의 P(θ)는 낮고, 능력이 높은 집단의 P(θ)는 높음을 나타내는’이라는 말은 ‘능력’과 ‘P(θ)’가 비례 관계임을 말한 것이다. 이를 고려해 문제의 <보기>에서 왜 그래프 I, Ⅱ, Ⅲ이 우상향 곡선인지를 이해하면 된다. 난이도는 위치 모수로 … 변별도는 척도 모수로 나타난다.
지문에서 ‘위치 모수’는 ‘문항의 P(θ)가 0.5일 때 그에 대응하는 지점’이라고 하였으므로, ‘문항의 P(θ)’ 즉 y축을 먼저 생각하고 x축 지점을 찾는 과정이 필요한 개념이다. 이를 이해했다면 <보기>의 그래프 I, Ⅱ는 위치 모수가 같고, 0.5에서 뻗어 나온 점선을 연장해 그것과 그래프 Ⅲ이 만나는 점의 x축의 지점(실제로 그래프에서 찾아보면 약 1이다)이 위치 모수임을 확인할 수 있다. 또한 지문에서 ‘위치 모수는 오른쪽에 있을수록 어려운 문항으로 추정된다’고 했다. 그에 따라 ‘난이도’가 1번, 2번 문항은 같고, 3번 문항은 그보다 어려움을 이해해야 한다.
그래프의 기울기는 변화율을 나타낸다. 지문에서 ‘변별도는 척도 모수로 나타난다. 척도 모수는 문항 특성 곡선의 기울기가 가파를수록 높다’고 했으므로, ‘척도 모수’와 ‘기울기’ ‘기울기’와 ‘변별도’는 비례 관계다. 그런데 그래프의 기울기를 파악할 때 구간별로 해야 할 경우가 있다. <보기>에서 θ가 0일 때를 기준으로 그래프 I, Ⅱ의 기울기가 정반대다. 이를 해석하면 피험자의 능력이 낮을 때는 1번 문항이 2번 문항보다 변별도가 ‘상대적’으로 높은 데 반해 피험자의 능력이 높을 때는 그 반대라는 뜻이다. 포인트
'A는 B에 따라 (그래프)로 그려지다' 라는 문장은 함수를 나타낸다는 것을 알아두자.<hr style="display:block !important; margin:25px 0; border:1px solid #c3c3c3" />'정규 분포'는 도수(度數) 분포 곡선이 평균값을 중앙으로 하여 좌우 대칭인 분포로서, 종 모양의 그래프로 표현됨을 알아두자.<hr style="display:block !important; margin:25px 0; border:1px solid #c3c3c3" />삽화는 국어 선생님이 친절을 베푼 것이므로, 삽화에 메모하며 글을 읽는 습관을 기르자.<hr style="display:block !important; margin:25px 0; border:1px solid #c3c3c3" />'증가함수'는 변수들이 비례 관계에 있음을 말하며 그래프가 우상향 형태로 표현됨을 알아두자.<hr style="display:block !important; margin:25px 0; border:1px solid #c3c3c3" />그래프의 기울기를 파악할 때 구간별로 해야 할 경우가 있음을 알아두자.관련뉴스
