②→⑤→복수정답(②⑤)→⑤로 3차례 걸쳐 변경
학교 당국 "혼선 빚어 학생들에게 사과"

(서울·군포=연합뉴스) 임화섭 오예진 기자 = 경기도의 한 고교가 중간고사 출제 실수로 정답 처리 방침을 세 차례나 바꾸면서 오락가락한 데 대해 학생들과 학부모들에게 사과했다.
대학 진학에서 내신의 중요성이 커지면서 학생들과 학부모들이 학교 성적 처리에 극도로 민감해진 가운데 일어난 일이다. 결국 명확한 결론이 나오긴 했으나, 학교가 갈팡질팡하면서 학생들과 학부모들이 혼란을 겪었다.
20일 경기도교육청 등에 따르면 이 교육청 산하의 한 공립 일반고는 지난달 23일에 1학년 1학기 수학 중간고사를 치른 직후 제16번 문항의 정답을 '② ㄱ, ㄴ'으로 발표했다.
그러나 이의제기 과정에서 문제에 [보기]로 제시된 'ㄱ, ㄴ, ㄷ' 셋 다 옳으므로 수학적으로 유일한 올바른 답이 '⑤ ㄱ, ㄴ, ㄷ'라는 지적이 나왔다. 이론(異論)의 여지가 없이 정확한 지적이었다.
출제 교사는 ㄱ, ㄴ에는 옳은 내용을, ㄷ에 틀린 내용을 각각 넣어서 답을 ②로 하려고 생각했으나, 착각으로 ㄷ에도 옳은 내용을 넣어 버리는 바람에 ⑤가 올바른 답이 된 것이다. '출제 실수'가 있었으나 문항을 놓고 보면 답이 명확했다.
이에 따라 학교 당국은 5월 1일과 2일에 교과협의회를, 3일에 성적관리위원회를 각각 열어 정답을 ⑤로 정정했다.
그랬더니 이번에는 ②도 인정해 달라는 이의제기가 들어왔다.
수학적으로는 엄연히 ㄷ이 옳으므로 ②는 정답이 아니지만, 교과과정의 순서상 ㄷ이 옳다는 점을 선뜻 이해하는 데 어려움을 겪어서 ②를 고른 학생들이 있을 수 있다는 점을 감안해 달라는 이유였다.
이 학교는 9일에 경기교육청 측 컨설팅을 받은 후 교과협의회를 열고 10일에 성적관리위원회를 다시 개최해 "'메인 정답'은 '② ㄱ, ㄴ'이며 복수정답 내지 유사정답으로 '⑤ ㄱ, ㄴ, ㄷ'을 인정한다"는 취지로 정답 처리 방침을 또 변경했다.
이런 사연이 지난 주에 엠엘비파크 등 인터넷 커뮤니티 게시판과 소셜 미디어를 통해 급속히 퍼져 나가면서 "복수정답 인정은 말도 안 되는 결정"이라는 비판이 네티즌들과 전문가들 사이에 거세게 일었다.
사이버 공간에서 논란이 불붙은 16∼17일 연합뉴스가 의견을 요청한 관련 분야 전문가들은 한결같이 수학의 학문적 관점뿐만 아니라 교육적 관점에서도 역시 ⑤를 유일한 정답으로 인정하는 것이 당연하다고 지적했다.
이학박사 겸 교육학박사로 수학과 교육학 양 분야의 전문가인 이승훈 유원대 교수는 "해당 내용은 1학년 2학기 집합과 명제 단원에서 '진리집합'을 배워야만 알 수 있는 것이 아니라, 초등학교와 중학교에서 다루는 부등식의 성질에서 이미 나오는 것"이라고, 정경훈 서울대 기초교육원 강의교수는 "교육상 수학적으로 옳은 유일한 결론만을 답으로 해야 한다"고 각각 설명했다.
이 고교 관계자들은 15일 취재차 학교를 방문한 연합뉴스 탐사보도팀 기자들을 만나 비판 의견을 전달받고 나서 정답 처리 방침을 세번째로 재검토하기 시작했다.

학교 당국은 15일과 16일에 교과협의회를 열고 외부 자문단의 추가 컨설팅을 받은 후 17일 교내 성적관리위원회를 열어 ⑤를 유일한 정답으로 인정하는 결정을 내렸다. 이어 학교 당국은 20일 정답 정정 사실을 학생들에게 알리고 혼선을 빚은 점을 사과했으며, 가정통신문도 발송했다.
학교 관계자는 "중간고사 시험 범위를 열심히 공부했는데도 익숙하지 않을 수 있는 내용이 있어서 잘못 판단한 학생들이 있을 수 있다는 점을 고려해 한때 복수정답을 인정하려고 했으나, 수학적으로 옳은 내용을 따르는 것이 교육적으로도 올바르며 교과과정 밖이라고 할 수도 없다는 결론을 내렸다"며 "혼란에 대해 학생들에게 사과한다"고 설명했다.
다음은 한 달도 안 되는 기간에 ②→⑤→복수정답인정(②⑤)→⑤로 정답 처리 방침이 갈팡질팡했던 문항의 전문과 그 풀이다.
[문항]
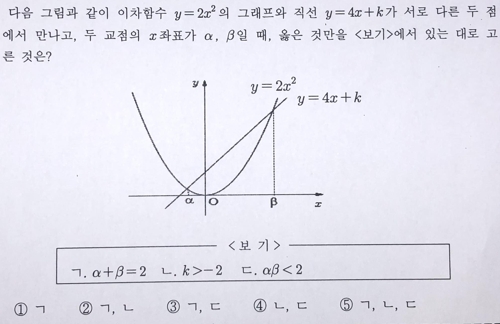
다음 그림과 같이 이차함수 y = 2x²의 그래프와 직선 y = 4x + k가 서로 다른 두 점에서 만나고, 두 교점의 x좌표가 α, β일 때 (보기)에서 옳은 것만을 있는 대로 고른 것은? [4.8점]
---------------
(보기)
ㄱ. α + β = 2
ㄴ. k > -2
ㄷ. αβ < 2
----------------
① ㄱ
② ㄱ, ㄴ
③ ㄱ, ㄷ
④ ㄴ, ㄷ
⑤ ㄱ, ㄴ, ㄷ
[풀이] (연합뉴스 제공)
x에 대한 실계수 이차방정식 2x²= 4x + k, 즉 (x - 1)²= 1 + k/2 이 서로 다른 두 실근 α, β를 가지므로, 1 + k/2 > 0 이다. 따라서
k > -2 …㈎
이다.
또 이차방정식의 근과 계수의 관계로부터
α + β = 2 …㈏
αβ = - k/2 …㈐
임을 알 수 있다.
따라서 보기에 나온 ㄱ, ㄴ, ㄷ 중에서 ㈏와 내용이 같은 ㄱ은 옳고, ㈎와 내용이 같은 ㄴ도 옳다.
또 ㈐와 ㈎로부터 αβ = - k/2 < 1임도 명백하다. 실수 α, β의 곱인 실수 αβ와 실수 1과 실수 2의 대소관계를 따져 보면, αβ < 1 < 2이므로, 부등식의 성질에 의해 당연히 αβ < 2라는 부등식, 즉 ㄷ도 성립한다.
그러므로 보기에 제시된 ㄱ, ㄴ, ㄷ 등 셋 다가 옳으며, 문항에 제시된 선택지 중 정답은 '⑤ ㄱ, ㄴ, ㄷ'이다.
solatido@yna.co.kr, ohyes@yna.co.kr
※ 편집자주 = 연합뉴스 탐사보도팀은 지난해 7월 '내신성적 믿을 수 있나' 기획(http://www.yonhapnews.co.kr/issue/3002000000.html?page=4&ctype=A&id=IC20181903)을 내보낸 이후 일선 학교의 내신성적 관리 실태에 관한 제보를 꾸준히 받고 있습니다. 이메일 investigative@yna.co.kr로 제보 내용을 보내 주시기 바랍니다.
(끝)
<저작권자(c) 연합뉴스, 무단 전재-재배포 금지>
관련뉴스













