그런데 가끔 동일한 현상을 놓고 서로 반대되는 주장을 지지하는 ‘과학적 데이터’가 등장하고, 우리는 주장하는 사람의 논리에 이러저리 이끌려다니고 있음을 뒤늦게 느낄 때가 있다. 왜 이런 상황을 겪고 있으며, 어떻게 우리 스스로 중심을 잡고 ‘과학적 데이터’를 이해할 수 있을까?
 자연과학적 대상이든 사회과학적 대상이든 무엇인가를 측정할 때는 그 측정값에 이름을 정해주고, 그 의미를 수학적으로 정확하게 정의한다. 일반적으로 그 정의는 수치로 표현할 수 있다. 그런데, 이 측정값이 방송이나 신문과 같이 대중적인 글에 인용될 때 그 정의와 표현 방법까지 엄격하게 제시되지는 않을 때가 많다.
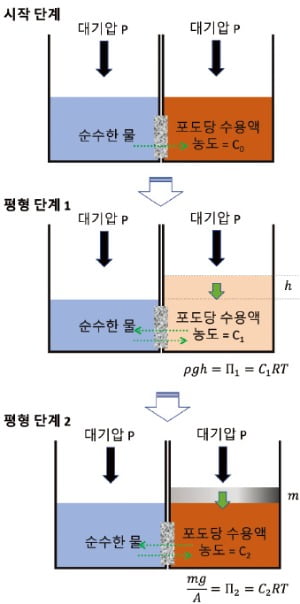
자연과학적 대상이든 사회과학적 대상이든 무엇인가를 측정할 때는 그 측정값에 이름을 정해주고, 그 의미를 수학적으로 정확하게 정의한다. 일반적으로 그 정의는 수치로 표현할 수 있다. 그런데, 이 측정값이 방송이나 신문과 같이 대중적인 글에 인용될 때 그 정의와 표현 방법까지 엄격하게 제시되지는 않을 때가 많다.예를 들어 살펴보자. 삼투압이라는 용어는 과학적으로 정의된 전문적인 개념이지만, 일상생활에서 편하게 통용되는 용어이기도 하다. 삼투압은 물은 잘 통과하지만 물속의 다른 물질은 잘 통과하지 않는 반투과성 막을 경계로 물이 한쪽으로 이동하는 현상의 결과로 나타나는 수압을 나타낸다. 삼투압의 정의를 <그림>으로 나타내면 다음과 같다. ‘시작 단계’는 왼쪽에 순수한 물이 있고 오른쪽에는 포도당 수용액(농도: Cο)이 있고 두 용기 사이에 반투막이 있어서 물 분자만 통과할 수 있고 포도당 분자는 통과할 수 없는 상황을 나타낸다. 이렇게 반투막을 경계로 농도가 다른 두 용액이 접하고 있는 상황에서 물이 왼쪽에서 오른쪽으로 이동하는 현상을 ‘삼투’ 현상이라고 한다.
왼쪽의 물이 오른쪽으로 이동하면 양쪽의 수면 높이가 차이 난다. 그렇다고 계속 이동하는 것은 아니고 어느 정도 높이 차이(h)가 나면 더 이상 변화가 없게 된다(평형 상태 1). 이 상태는 오른쪽의 물기둥 높이에 의한 압력(P=ρgh)과 삼투 현상에 의한 압력(Π)이 균형을 이루는 것으로, 이 관계를 이용해 다음과 같이 삼투압을 정의할 수 있다. 이때, C₁은 평형 상태에서 오른쪽의 포도당 농도이고, R은 상수이고 T는 온도다.
ρgh=Π₁=C₁RT
평형 상태 1에서 질량 m의 추를 얹어서 추가 압력을 가하면 포도당 용액의 수위가 다시 원위치로 돌아오게 할 수 있다. 이 상태는 평형 상태 1과는 다른 평형 상태로 반투막을 경계로 물 분자의 이동은 서로 균형을 이루고 있다(평형 상태 2). 마찬가지로 이 관계를 이용해 다음과 같이 삼투압을 정의할 수 있다. C₂는 평형 상태에서 오른쪽의 포도당 농도이고, A는 힘을 받는 단면적이다.
mg/A=Π₂=C₂RT
두 평형 상태를 기반으로 정의한 삼투압의 정량적 표현은 Π=CRT로 포도당 농도에 의해서 동일한 형태로 정의된다. 하지만, 평형 상태 1과 평형 상태 2에서 포도당 용액의 부피가 다르기 때문에 두 평형 상태에서 농도 C₁과 C₂가 차이 있고(C₁이 C₂보다 작다), 그 차이로 삼투압 값도 차이가 난다. 즉, 삼투압을 정의하는 방법에 따라서 그 수치가 달라진다.
TV 방송 또는 신문 기사와 같이 일반적인 상황에서 삼투압을 언급할 때는 두 값의 차이가 크지 않기 때문에 어느 정의에 의한 값인지는 크게 중요하지 않다. 그런데 매우 정확하고 정밀한 값을 필요로 할 때는 언급하는 삼투압 수치가 어떤 정의에 따라 측정된 값인지 고려하지 않으면 정확한 의미를 해석할 수 없게 된다.
다른 측면에서 살펴보면 특정 물질 자체가 위험한지 아닌지를 판단하는 것이 아니고 물질의 종류와 그 양을 함께 고려해 판단하고 있음을 알 수 있다. 극단적인 예로, 음식에 절대 빠질 수 없는 소금을 두고 위험한 물질이라고 하지는 않지만, 하루 평균 섭취량이 2g이 넘으면 건강에 위험한 물질이 된다. 반대로, 염산은 산의 세기가 매우 커서 위험한 물질이지만 100만 배 정도 희석하면 식초보다 산성이 낮게 된다. 즉, 독성이 강한 물질도 노출되는 양이 적으면 독성이 없거나 악영향이 나타나지 않고, 반대로 독성이 매우 낮은 화학물질도 많은 양을 섭취하면 건강상 문제가 발생할 수 있다.
 과학적 데이터가 의미하는 바는 누군가가 해석해주는 의미에 한정되지 않는다. 때에 따라서는 측정값이 어떻게 정의됐는지를 살펴봐야 할 때도 있다. 데이터의 해석이 ‘참’과 ‘거짓’ 또는 ‘좋음’과 ‘나쁨’ 사이의 판단에 있을 때는 실제 그렇게 이분법적인 의미가 아닐 수 있음도 살펴야 한다. 또 데이터가 의미하는 바에 대한 주된 의미가 제공될 때, 그런 의미만 있는 것이 아니고 다른 측면의 해석도 함께 있을 수 있음을 살펴봐야 한다. 이런 비판적인 시각을 가지고 과학적 데이터를 만날 때 과학적 데이터와 제대로 소통할 수 있다.
과학적 데이터가 의미하는 바는 누군가가 해석해주는 의미에 한정되지 않는다. 때에 따라서는 측정값이 어떻게 정의됐는지를 살펴봐야 할 때도 있다. 데이터의 해석이 ‘참’과 ‘거짓’ 또는 ‘좋음’과 ‘나쁨’ 사이의 판단에 있을 때는 실제 그렇게 이분법적인 의미가 아닐 수 있음도 살펴야 한다. 또 데이터가 의미하는 바에 대한 주된 의미가 제공될 때, 그런 의미만 있는 것이 아니고 다른 측면의 해석도 함께 있을 수 있음을 살펴봐야 한다. 이런 비판적인 시각을 가지고 과학적 데이터를 만날 때 과학적 데이터와 제대로 소통할 수 있다.관련뉴스














